本文收录于2019年3月的洛谷日报，原文初稿于 2019-01-20.
WBLT 全称 \(\text{Weight Balanced Leafy Tree}\). 是一种常数较小，代码较简单的平衡树实现方式。
在看本文之前，推荐您先学习 treap 等平衡树 这篇文章对于有平衡树基础的人较为友好
定义和引入
WBLT是二叉搜索树的一种。不同的是，他同时是一个大根堆（也可以是小根堆），每个非叶节点都有两个儿子，且每个节点的权值与其右儿子的权值相同，且左儿子的权值小于右儿子的权值，左子树的所有节点的权值小于右子树任意节点的权值。
也就是说他大概长这样：
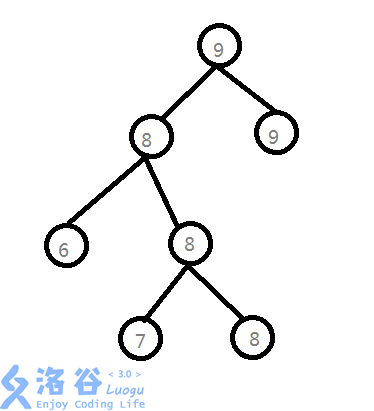
这种设计有一个明显的缺点 就是如果要储存n个数据，普通的平衡树需要开n个节点，而WBLT需要开2n-1个
也就是说 储存上图的数据的treap长这样：
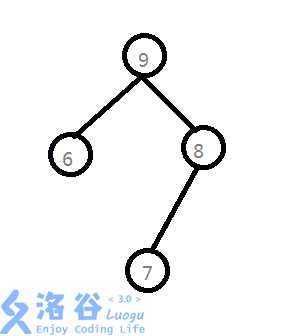
那么 相比之下它有什么好处呢？
旋转
WBLT= Weight Balanced Tree（加权平衡树） + Leafy，其中Leafy已经在定义和引入中体现了，平衡是指一个节点的左子树和右子树大小近似相同，这样在查询/修改的时候才能做到近似log，旋转便是维护平衡的方便手段
因为其结构特殊 不需要像treap一样引入一个rand，只要旋转就可以维护其平衡。
先给出旋转的代码 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| inline void merge(int l,int r){
size[++cnt]=size[l]+size[r];
val[cnt]=val[r];
ls[cnt]=l,rs[cnt]=r;
}
inline void rotate(int cur,bool flag){
if(flag){
merge(ls[cur],ls[rs[cur]]);
ls[cur]=cnt;
rs[cur]=rs[rs[cur]];
}
else{
merge(rs[ls[cur]],rs[cur]);
rs[cur]=cnt;
ls[cur]=ls[ls[cur]];
}
}
|
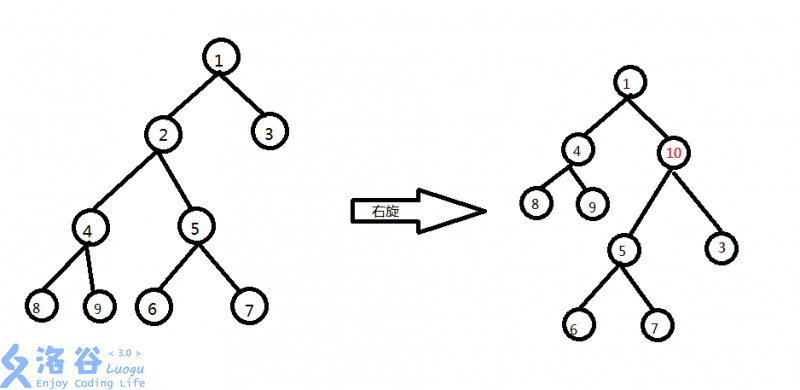可以发现，旋转后的WBLT仍然保持原来的性质。而且明显偏重的左子树转到了右边，左右子树相对平衡了。
查询排名为x的数
我们记录每个节点的size，这个size不是子树的大小，而是子树储存的有效信息的大小。
因为有性质_储存n个数据要开2n-1个节点_，所以如果一个子树的大小为\(2x-1\)，那它储存的数据量就有\(x\)个。
接下来的操作就简单了，令find(cur,x)为寻找cur所在的子树下排名为x的数，那么当x比左子树的size小
\(find(cur,x)=find(lson_{cur},x)\)
当x比左子树的size大
$find(cur,x)=find(rson_{cur},x-size_{lson_{cur}})
如果相等，那显然
\(find(cur,x)=val_{cur}\)
因为当前要找的是第x大，那我无需遍历下面，这点也与treap不同
1
2
3
4
5
6
7
| int find(int cur,int x){
if(size[cur]==x)
return val[cur];
if(x>size[ls[cur]])
return find(rs[cur],x-size[ls[cur]]);
return find(ls[cur],x);
}
|
查询x的排名
同理，设rnk(cur,x)为寻找cur子树下x的排名
当x小于cur的左儿子的权值
\(rnk(cur,x)=rnk(lson_{cur},x)\)
否则
\(rnk(cur,x)=size_{lson_{cur}}+rnk(rson_{cur},x)\)
1
2
3
4
5
6
7
| int rnk(int cur,int x){
if(size[cur]==1)
return 1;
if(x>val[ls[cur]])
return rnk(rs[cur],x)+size[ls[cur]];
return rnk(ls[cur],x);
}
|
插入
WBLT其他的操作都与treap类似，在每一步时：
根据要添加的权值和当前搜索到的节点选择左右子树进行递归（如果比左儿子的权值大就去右子树，否则去左子树）
递归到最后一步到一个叶子节点时，根据其权值大小建立新节点，确定是该节点的左儿子还是右儿子
建立它的兄弟节点。
向上pushup（类似于线段树，儿子会影响父亲，这点于与treap不同）。
1
2
3
4
5
6
7
8
9
10
| void insert(int cur,int x){
if(size[cur]==1){
newnode(ls[cur],minn(x,val[cur]));
newnode(rs[cur],maxx(x,val[cur]));
pushup(cur);
return ;
}
insert(x>val[ls[cur]]?rs[cur]:ls[cur],x);
pushup(cur);
}
|
删除
在每一步时：
根据要删除权值和当前搜索到的节点选择左右子树进行递归（如果比左儿子的权值大就去右子树，否则去左子树）
递归到最后一步到一个叶子节点时，判断该节点是不是要删除的，如果不是则选择其兄弟节点，进行删除，将两个节点中保留的与其父亲节点进行替换
向上pushup。
1
2
3
4
5
6
7
8
9
10
| void erase(int cur,int x){
if(size[cur]==1){
cur= ls[fa]==cur?rs[fa]:ls[fa];
copynode(fa,cur);
return ;
}
fa=cur;
erase(x>val[ls[cur]]?rs[cur]:ls[cur],x);
pushup(cur);
}
|
旋转，和P3369
等等 旋转呢？
我们在上文所有的操作中，似乎没有使用旋转，那旋转放在哪呢？
我们将其放在树的结构有改变的地方，也就是插入 删除这些操作中，每当一个子树过大，就进行相应的旋转，在插入和删除操作中加入以下函数即可
1
2
3
4
5
6
7
8
| const int ratio=5;
inline void maintain(int cur){
if(size[ls[cur]]>size[rs[cur]]*ratio)
rotate(cur,0);
else if(size[rs[cur]]>size[ls[cur]]*ratio)
rotate(cur,1);
}
|
那么普通平衡树的代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
| #include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int maxn=400010;
const int ratio=5;
int n,cnt,fa,root;
int size[maxn],ls[maxn],rs[maxn],val[maxn];
inline void newnode(int &cur,int v){
cur=++cnt;
size[cur]=1;
val[cur]=v;
}
inline void copynode(int x,int y){
size[x]=size[y];
ls[x]=ls[y],rs[x]=rs[y];
val[x]=val[y];
}
inline void merge(int l,int r){
size[++cnt]=size[l]+size[r];
val[cnt]=val[r];
ls[cnt]=l,rs[cnt]=r;
}
inline void rotate(int cur,bool flag){
if(flag){
merge(ls[cur],ls[rs[cur]]);
ls[cur]=cnt;
rs[cur]=rs[rs[cur]];
}
else{
merge(rs[ls[cur]],rs[cur]);
rs[cur]=cnt;
ls[cur]=ls[ls[cur]];
}
}
inline void maintain(int cur){
if(size[ls[cur]]>size[rs[cur]]*ratio)
rotate(cur,0);
else if(size[rs[cur]]>size[ls[cur]]*ratio)
rotate(cur,1);
}
inline void pushup(int cur){
if(!size[ls[cur]])return ;
size[cur]=size[ls[cur]]+size[rs[cur]];
val[cur]=val[rs[cur]];
}
inline int minn(int a,int b){
return a<b?a:b;
}
inline int maxx(int a,int b){
return a>b?a:b;
}
inline void insert(int cur,int x){
if(size[cur]==1){
newnode(ls[cur],minn(x,val[cur]));
newnode(rs[cur],maxx(x,val[cur]));
pushup(cur);
return ;
}
maintain(cur);
insert(x>val[ls[cur]]?rs[cur]:ls[cur],x);
pushup(cur);
}
inline void erase(int cur,int x){
if(size[cur]==1){
cur= ls[fa]==cur?rs[fa]:ls[fa];
copynode(fa,cur);
return ;
}
maintain(cur);
fa=cur;
erase(x>val[ls[cur]]?rs[cur]:ls[cur],x);
pushup(cur);
}
inline int find(int cur,int x){
if(size[cur]==x)
return val[cur];
maintain(cur);
if(x>size[ls[cur]])
return find(rs[cur],x-size[ls[cur]]);
return find(ls[cur],x);
}
inline int rnk(int cur,int x){
if(size[cur]==1)
return 1;
maintain(cur);
if(x>val[ls[cur]])
return rnk(rs[cur],x)+size[ls[cur]];
return rnk(ls[cur],x);
}
int main(){
scanf("%d",&n);
newnode(root,(1<<30));
while(n--){
int s,x;
scanf("%d%d",&s,&x);
if(s==1)insert(root,x);
if(s==2)erase(root,x);
if(s==3)printf("%d\n",rnk(root,x));
if(s==4)printf("%d\n",find(root,x));
if(s==5)printf("%d\n",find(root,rnk(root,x)-1));
if(s==6)printf("%d\n",find(root,rnk(root,x+1)));
}
return 0;
}
|
以下是评测记录
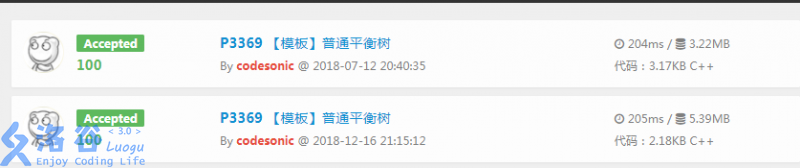
上面的是treap，下面的是WBLT
我们发现，WBLT只比treap慢一点点，所以WBLT和treap几乎是一样块的~
例题
P1503 鬼子进村
平衡树部分是个裸题，其他倒还得想想
先把0和n+1插入，作为边界
摧毁节点就插入该点
删除上一个就维护个栈，删除栈顶即可
询问操作就查找前驱和后继，一减就行了，记得特判是否已经被摧毁（记个vis数组即可）
代码
P2596 [ZJOI2006]书架
平衡树部分还是个裸题
定义优先级越小，那本书就放越上面
设\(a_i\)为编号为\(i\)的书本的优先级，\(mapp_i\)为优先级为i的节点编号。
Top S:将优先级变为最小再插入
Bottom S：将优先级变为最大再插入
Insert S T：找到对应两本书 交换优先级
Ask S：查询优先级排名
Query S：查询第k小的优先级对应的编号
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
| #include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<map>
using namespace std;
const int maxn=400010;
const int ratio=5;
inline int read(){
register int num=0,flag=1;char ch;
while((ch=getchar())<'0'||ch>'9') if(ch=='-') break;
if(ch=='-') flag=-1;
else num=ch-'0';
while((ch=getchar())>='0'&&ch<='9') num=num*10+ch-'0';
return num*flag;
}
void out(int x){
if(x>=10) out(x/10);
putchar(x%10+'0');
}
int n,m,cnt,fa,root;
int size[maxn],ls[maxn],rs[maxn],val[maxn],a[maxn];
int mapp[maxn];
char opt[20];
int k,l,r,i;
int main() {
n=read();
m=read();
newnode(root,(1<<30));
l=233333,r=n+233333;
for(i=1; i<=n; i++) {
int qaq;
qaq=read();
insert(root,i+233333);
a[qaq]=i+233333;
mapp[i+233333]=qaq;
}
while(m--) {
scanf("%s",opt);
if(opt[0]=='Q') {
k=read();
out(mapp[find(root,k)]);
putchar('\n');
} else if(opt[0]=='A') {
k=read();
out(rnk(root,a[k])-1);
putchar('\n');
} else if(opt[0]=='T') {
k=read();
erase(root,a[k]);
insert(root,--l);
a[k]=l;
mapp[l]=k;
} else if(opt[0]=='B') {
k=read();
erase(root,a[k]);
insert(root,++r);
a[k]=r;
mapp[r]=k;
} else if(opt[0]=='I') {
register int s=read(),t=read();
if(t==1) {
int rnk2=rnk(root,a[s]),rnk1=rnk2+1;
int s2=find(root,rnk1);
s2=mapp[s2];
erase(root,a[s]);
erase(root,a[s2]);
swap(a[s],a[s2]);
mapp[a[s]]=s;
mapp[a[s2]]=s2;
insert(root,a[s]);
insert(root,a[s2]);
} else if(t==-1) {
int rnk2=rnk(root,a[s]),rnk1=rnk2-1;
int s2=find(root,rnk1);
s2=mapp[s2];
erase(root,a[s]);
erase(root,a[s2]);
swap(a[s],a[s2]);
mapp[a[s]]=s;
mapp[a[s2]]=s2;
insert(root,a[s]);
insert(root,a[s2]);
}
}
}
return 0;
}
|
结果这个吊打了splay ，和fhq-treap差不了多少
而且似乎比同种思路的treap快了300ms左右
总结
WBLT有着显著的优缺点
优点是快（ \(\text{O}(n\log n)\) 常数较小） 好记 码量小 且能实现很多功能
缺点是内存空间大，尽管可以用垃圾回收补偿，但是仍然需要两倍的空间
备注：本文实现方法是单旋，没法证复杂度同时也难以卡掉。2018集训队论文里介绍了双旋的实现，是复杂度正确的。
