本文原稿初稿于2019-11-17，搬运过来作参考。

基础知识

排列组合

排列

从$n$个数字有序地选择$k$个数字的方案数。

第一个数字有$n$种选择方案，第二个有$n-1$

于是答案为$n(n-1)(n-2)...(n-k+1)=\frac{n!}{(n-k)!}=n^{\underline{k}}$。($n^{\underline{k}}$指n的k次下降幂）

记为$P_n^k,A_n^k,{n\choose k}*k!$

前两个好像是苏联的符号...?

组合

从$n$个数字个数字无序地选择$k$个数字的方案数。

因为无序，在排列的基础上除以$k!$即可

记为$C_n^k,{n\choose k}$

同样地，国际上都喜欢用第二种。

二项式定理

$(x+1)^n$中$x^k$前的系数。

等价于$n$个单项式中选$k$个取$x$，其余取$1$

展开式：

\[(x+y)^n=\sum_{k=0}^n{n \choose k}x^ky^{n-k}\]

广义二项式定理

求$(x+y)^a$ （a是有理数）

\[(x+y)^a=\sum^{\infty}_{k=0}\frac{a^{\underline{k}}}{k!}x^ky^{(a-k)}\]

如果是正整数显然能那个分数能对应成刚刚的组合数

其他情况要泰勒展开，我不会。

隔板法

n个一样的球放进m个不同的盒子，能不放，求方案数

把n个东西划分成m段，可以强行加m个球要求不能不放，那么就是在n+m-1个划分点选m-1个

答案为${n+m-1 \choose m-1}={n+m-1 \choose n}$

以上是最简单的排列组合，下面的东西可能会让人懵掉。

计数原理

抽屉原理

把$kx+b(0<b<x)$个物品放进$x$个盒子内，至少有一个盒子内有$k+1$个东西

加法原理

事件$A$有$n$个结局，事件$B$有m种结局，发生了一个事件，共有$(n+m)$种结局

若干不交的集合取一个的方案数，等于集合大小的和。

乘法原理

事件$A$有$n$个结局，事件$B$有$m$个结局，两个事件都发生了，共有$nm$种结局

若干不交的集合格取一个的方案数，等于集合大小的乘积。

以上计数原理是计数的基石，虽然很浅显但是在后面的知识中扮演关键的角色、

特殊数列

卡特兰数

定义式：

\[h_n=\sum^{n-1}_{k=0}h_kh_{n-1-k}(h_0=h_1=1)\]

通项式：

\[h_n={2n \choose n}-{2n \choose n-1}=\frac{2n \choose n }{n+1}\]

应用场景很多

括号序列数量，$n\times n$方格行走数（不能越过对角线），凸多边形划分数，二叉树数量

用方格行走推导 $h_n = {2n n} - {2n n-1} $ ：

将模型转换成这样：

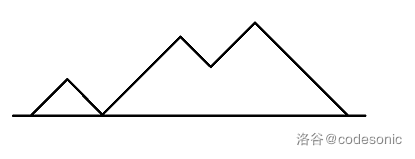
然后不能越过下面的直线

我们要走n次向上，n次向下，共2n次，这样我们才能回到0。

先忽略不能越过下面的直线，那就是在2n步中选出n步向上走，为${2n \choose n}$

接下来减掉不合法的，如果越过了这个线，那么这时我们把终点(n,0)，改成(n,,-2)，进行一次翻转，就只需要走n+1步向下，n-1步向上，答案为${2n \choose n-1}$，这是一个反射法的经典应用。

${2n \choose n}-{2n \choose n-1}=\frac{2n \choose n}{n+1}$ 可以用数学方法证明~~留与读者自证~~

第一类斯特林数

用$S_u(n,m)$表示n个不同元素构成m个圆排列的方案数

1.最后一个元素单独做环

2.插入之前的m个环中

\[S_u(n,m)=S_u(n-1,m-1)+(n-1)*S_u(n-1,m)\]

第一类斯特林数有时候有符号，在生成函数上应用较多，记为$S_s$

\[S_s(n,m)=(-1)^{n+m}S_u(n,m)\]

有符号的斯特林数的生成函数为$x^{\underline{n}}$，这个结论非常重要，有了这个可以快速求斯特林数

建议明白生成函数后再回来看

第二类斯特林数

$S(n,m)$表示把$n$个不同元素拆分进$m$个非空集合的方案数，集合不为空

\[S(n,m)=S(n-1,m-1)+m*S(n-1,m)\]

类似于第一类斯特林数，考虑当前元素再新建一个集合和加入之前的集合即可。

\[S(n,m)=\frac{1}{m!}\sum(-1)^k{m \choose k}(m-k)\]

这个式子可以用卷积快速计算，但是因为本篇主题是计数，所以不展开。

贝尔数（不要求划分成几个集合）是第二类斯特林数之和。

拆分数

$f_n$表示大小为n的正整数拆分成若干无序的正整数和的方案数

有两种DP方法

1$.f_{i,j}$表示拆分成若干不超过j的方案数

\[f_{i,j}=f_{i-j,j}+f_{i,j-1}\]

2.$g_{i,j}$表示拆分j个数字的方案数

\[g_{i,j}=g_{i-1,j-1}+g_{i-j,j}\]

两个DP复杂度都是平方级别的。

考虑大小超过$\sqrt{n}$的数字最多只有$\sqrt{n}$个，结合两种DP，复杂度$O(n\sqrt{n})$

用第一个DP考虑小的数字，用第二个DP考虑大的数字，先用f算出$\sqrt{n}$以内的答案，g的方程就可以改为$g_{i,j}=g_{i-\sqrt{n},j-1}+g_{i-j,j}$

拆分数也有生成函数，为：

\[\frac{1}{\Sigma(-1)^kx^{k(3k\pm 1)}}\]

下面这个分母是带符号的五边形数

如果把拆分出来的正整数想象成柱形图，那么这两种方法一种是按列考虑，一种按行考虑。

生成函数

生成函数的应用简单来说在于研究未知（通项）数列规律，用这种方法在给出递推式的情况下求出数列的通项

多项式与形式幂级数

形式幂级数的定义：

\[\sum _{n\geq 0}a_nx^n\]

可以认为是一个有无穷次项的多项式，所有次项都为正

加减法：

\[\sum _{n\geq 0}a_nx^n\pm \sum _{n\geq 0}b_nx^n=\sum _{n\geq 0} (a_n\pm b_n)x^n\]

乘法：

\[\sum _{n\geq 0}a_nx^n\times \sum _{n\geq 0}b_nx^n=\sum_{n\geq 0}(\sum _{k=0}^na_kb_{n-k}x^n)\]

类似于多项式的加减法和乘法

闭形式

形式幂级数的表达形式是一个长度无穷的多项式，但是对于部分的形式幂级数，存在长度有限的函数能够直接表示它，则称之为闭形式。

比如等比数列：

\[\sum _{n \geq0}x^n=\frac{1}{1-x}\]

\[\sum _{n \geq1}x^n=x\sum _{n \geq0}x^n=\frac{x}{1-x}\]

意义：把无穷长度的形式幂级数改写为有限长度的闭形式

组合对象

组合计数是一类常见问题，通常给定我们若干组合条件，对于每个组合对象，有某个函数 $size$ 衡量了它的大小，如图的节点数，序列的长度等。$size$ 为 $n$ 的个数为有限个，记为$A_n $，求某个$A_n.$

这些图，序列等就是组合对象。

组合对象分为是否有标号的两种，指的是是否考虑组合对象内部的元素有不同的区别，例如无标号的三个点的图只有 4 种，而有标号的有 8 种。

普通生成函数

数列$A_0,A_1,A_2...$的普通生成函数为

\[\sum _{n \geq 0}A_nx^n\]

普通生成函数通常考虑无标号问题，它的加法操作和乘法操作分别对应了并和拼接两种操作。

斐波那契数

$f_n$表示第n个斐波那契数，求$\sum_{n \geq 0}f_nx^n$的闭形式

令

\[F(x)=\sum_{n\geq0}f_nx^n\]

由于$f_n=f_{n-1}+f_{n-2}$可得

\[F(x)=xF(x)+x^2F(x)+1\]

解方程得

\[F(x)=\frac{1}{1-x-x^2}\]

分解质因数后裂项，可得到通项公式。

卡特兰数

求节点数为n的二叉树个数

生成函数本身具有组合性质，令$F(x)$表示该问题的生成函数，一棵二叉树可以划分成根节点和左右子树，是两个完整都二叉树，

所以$F(x)=xF^2(x)+1$，解方程可得$F(x)=\frac{1-\sqrt{1-4x}}{2x}$

通过泰勒展开可以求得通项公式。

因为我不会也不是主题内容，所以不展开

指数生成函数

指数生成函数一般用来解决有标号问题

数列$A_0,A_1,A_2...$的指数生成函数为

\[\sum _{n \geq 0}\frac{A_n}{n!}x^n\]

连通图计数

考虑到任意图可以被划分成若干连通图。

定义连通图的生成函数为$F(x)$，任意图的生成函数为$G(x)$。

很容易求出任意图的生成函数，即

\[G(X)=\sum _{n\geq 0}\frac{2^{n(n-1)/2}}{n!}x^n\]

任意图是由连通图构成的，所以$G(x)=e^{F(x)}$，所以F(x)=ln G(x)，通过多项式姿势可以快速求出来

Polya定理

Burnside 引理

置换

置换就是对元素进行重新排列，必须（类似于线性代数中的线性映射）。

比如，把正方体旋转90度，可以看做四个顶点的一个置换

有以下结论：

置换可以构成环:从一个元素置换前到置换后连一条有向边，会构成环(循环）

定义一个状态S经过置换后与原来相同，则称其为不动点。

置换群

置换群指的是一个置换的集合，满足任意两个置换不能复合出一个新的不在集合内的置换。

Burnside 引理

令$X$表示某个集合，$G$表示某个作用在X上的某个置换群。对于任意$G$内的元素$g$，定义$f(g)$为$X$内经过置换$g$后不变的元素数量，我们要求$X$内本质不同的元素个数（本质不同指不能通过$G$获得彼此），这个个数记为$|X/G|$

（这也被称为等价类，求的也就是等价类个数）

形象地说，比如某个集合:

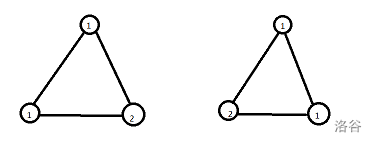
然后有一个置换为逆时针旋转60度，那这两个元素本质相同。

Burnside 引理为：

\[|X/G|=\frac{1}{|G|}\sum_{g\in G}f(g)\]

证明：

我们发现一个元素是不是不动点需要考虑两个东西：一是元素本身，二是置换，所以不动点是二元的

例子：

一个正方形分成4格,涂上黑白两种颜色,有多少种方案？其中经过转动相同图像的算一种方案

本来可以直接枚举，但是我们要验证Burnside ，所以对其加以考虑。

在这个正方形上的置换有：

(1)顺时针转90度，(2)逆时针转90度，(3)不动，(4)直接转动180度

先把所有正方形画出来

然后按从上到下从左到右一行一行编号为(1)~(16)

其中对于每个置换，列出不动点：

(1):2个

(2):2个

(3):16个

(4):4个

\[|X/G|=\frac{1}{|G|}\sum_{g\in G}f(g)=\frac{1}{4}(2+2+16+4)=6\]

Polya定理

设$G$是$X$的一个置换群，$|X|$=n，用$m$种颜色染色，本质不同的方案数:

\[L=\frac{1}{G}\sum_{g\in G}m^{c(g)}\]

$c(g)$表示$g$的循环节个数。

通常我们并不枚举所有的$g$，并计算$c(g)$，而是枚举 $c(g)$，快速计算多少$g$满足条件。

仍然将一个正方形分成4格,涂上黑白两种颜色,有多少种方案？其中经过转动相同图像的算一种方案

在这个正方形上的置换有：

不动：4

旋转90度：1

旋转180度：2

旋转270度：1

$M=\frac{1}{4}(2^4+2^1+2^2+2^1)=6$

生成树计数

度数矩阵，邻接矩阵和基尔霍夫(Kirchhoff)矩阵

对于一个无向图$G$，定义$G$的度数矩阵$D$满足：

\[d_{i,j}=\begin{cases} deg_i\space\space\space(i=j)\\0\space \space\space\space\space\space\space\space(i\ne j)\end{cases}\]

其中，$deg_i$表示节点i的度数

定义$G$的邻接矩阵$C$满足：

\[c_{i,j}=\begin{cases} 0\space\space\space\space\space\space\space\space\space\space(i=j)\\adj_{i,j}\space \space\space(i\ne j)\end{cases}\]

定义$G$的基尔霍夫矩阵$L$：$L=D-G$，也就是：

\[l_{i,j}=\begin{cases} deg_i\space\space\space\space\space\space\space\space(i=j)\\-adj_{i,j}\space \space\space(i\ne j)\end{cases}\]

行列式

定义：一个矩阵$A$的行列式表示为:

\[|A|=\sum _p(-1)^{\sigma(p)}\prod_{i=1}^na_{i,p_i}\]

性质：

1.一个对角矩阵/上三角矩阵的行列式值是所有对角线上元素的乘积。

2.交换矩阵的两行/两列，行列式值取反

3.将矩阵的一行/一列乘上一个固定的常数 k，行列式值也乘上 k。

4.将矩阵的一行加到另外一行上去，行列式值不变，列同理。

可以使用高斯消元快速计算行列式。

矩阵树(Matrix-Tree)定理

图$G$的生成树数量是依照以上步骤求出来的基尔霍夫矩阵$L$的行列式的任意一个代数余子式。

也就是说随意取它的任意一个$n-1$阶主子式，然后求出主子式的值，得到的就是在这个图中生成树的数量。

代码：咕咕咕

计数笔记就到这里结束了，以后可能会补一些例题什么的~

接下来大概要学线代和数论/多项式~